数学史上的传奇人物:高斯的整数、方程和分布
数学史上的传奇人物:高斯的整数、方程和分布
高斯被誉为“数学之王”,他是数学领域的传奇人物。在他短暂而辉煌的生涯中,他对数学领域做出了许多重要的贡献,其中代数学是他最擅长的研究方向之一。本文将深入介绍高斯在代数学中的成就,包括高斯整数、代数方程、线性代数、最小二乘法、复变函数、调和函数、概率论等方面,旨在让读者更好地了解代数学的基础概念和方法,以及高斯对该领域的重大贡献。
代数基础
代数学是一门研究关于代数系统的学科,其中包括了各种数学对象,例如整数、多项式、矩阵等等。代数学最基础的概念是代数结构,其中包括了群、环、域等等。高斯在代数学的研究中打下了基础,并提出了许多重要的概念和方法。
高斯整数
高斯整数是指形如 a+bi 的复数,其中 a 和 b 都是整数。高斯整数是一种特殊的整数环,它具有唯一分解定理,即每个高斯整数都可以唯一地表示为若干个质数的乘积。这使得高斯整数在数论中具有重要的应用,并且在代数学的研究中也起到了重要的作用。
例如,我们可以使用高斯整数来解决勾股定理中的无理数问题。例如对于勾股数 3, 4, 5我们知道其斜边长为
,但是如果我们考虑另一个勾股数 5,12,13则其斜边长为
,这就意味着该勾股数的斜边长是一个整数。而事实上,这个斜边长正是 5+12i,这就引出了高斯整数这一代数学对象。
代数方程
代数方程是指形如
的方程,其中
都是实数或复数。高斯著名的代数基本定理指出,每个代数方程都可以因式分解为若干个一次或二次的因式。同时,他还提出了各种求解代数方程的方法,例如平方根法和牛顿法等等。
例如对于二次方程
,我们可以应用高斯的求根公式进行求解。该公式表明,对于该方程的两个解
和
,有:
这一公式可以通过配方法推导得到,也可以通过高斯引入的复数概念进行证明。不管是哪种方式,都体现了高斯在代数方程研究中的重要贡献。
线性代数
线性代数是一门研究线性空间、线性变换和矩阵的学科。高斯对线性代数的研究做出了许多重要的贡献,例如高斯-约旦消元法和高斯-若尔当消元法等等。这些方法被广泛应用于各个领域,例如计算机图形学、机器学习和量子力学等等。
例如对于线性方程组 Ax=b,我们可以使用高斯-约旦消元法将其化为上三角矩阵形式,然后通过回代的方式求解出该方程组的解。这一方法在计算机科学和应用数学中广泛应用,并且也启发了其他线性代数方法的研究。
最小二乘法
最小二乘法是一种数学优化方法,用于拟合数据和估计误差。在许多实际问题中,我们需要从给定的数据中寻找一个最佳的函数模型,以便预测未知的数据。而最小二乘法就是一种常用的方法,它能够通过最小化数据点到拟合曲线的距离来确定最佳的函数模型。
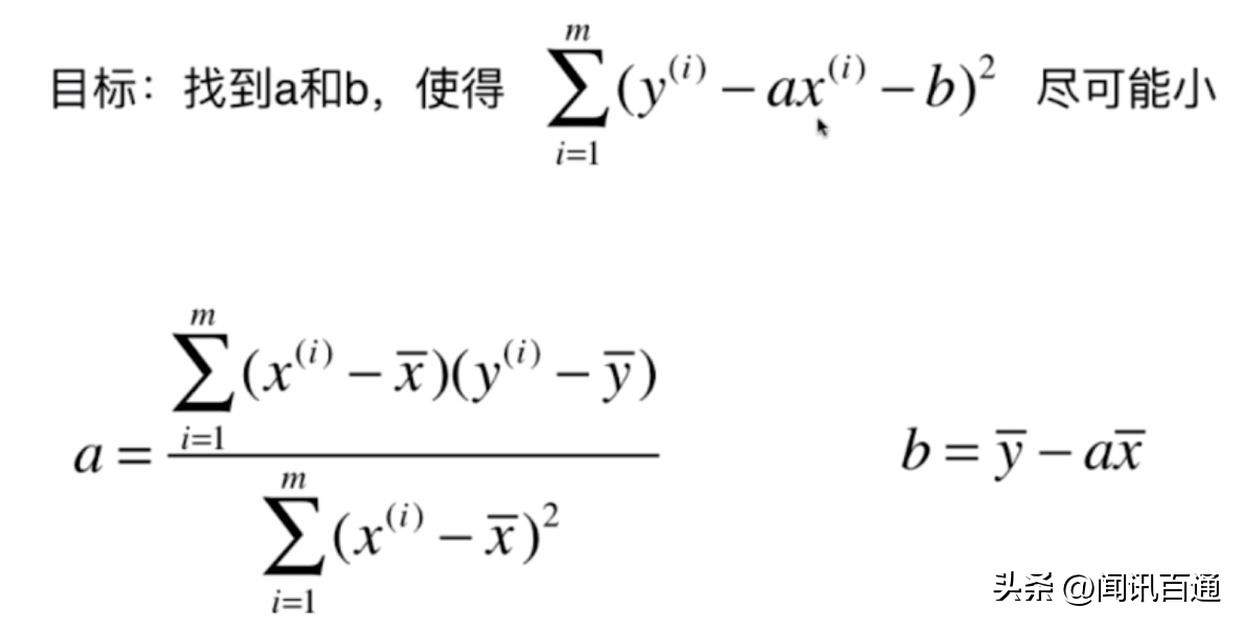
最小二乘法
高斯就是最小二乘法的创始人之一,他于1795年提出了这一方法,用于解决天文学和测量学中的拟合问题。他的贡献使得最小二乘法被广泛应用于各个领域,例如统计学、信号处理和机器学习等等。
复变函数和调和函数
复变函数
复变函数是指在复平面上定义的函数,它可以看作是两个实变量的函数,其中一个变量是实部,另一个变量是虚部。高斯在复变函数研究中提出了许多重要的概念和方法,例如全纯函数、调和函数和亚纯函数等等。
调和函数是一种特殊的复变函数,它满足某些微分方程,具有很多应用,例如电磁场、流体力学和声学等方面。高斯为调和函数的研究做出了重要贡献,并提出了一些解析结果,例如格林第一第二定理和柯西-黎曼方程等等。
概率论
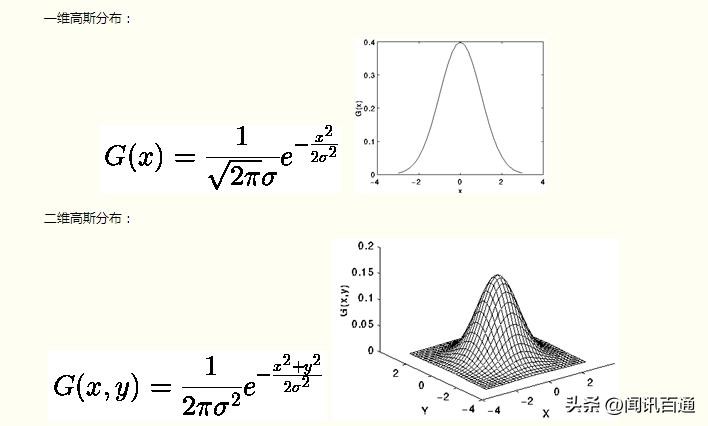
高斯也在概率论领域做出了一些贡献。他发明了高斯分布,成为了现代概率统计理论的基础之一。高斯分布是一种连续概率分布,具有钟形曲线,经常被用于描述各种自然现象和社会现象,例如身高、考试成绩和收入等等。
除此之外,高斯还研究了误差理论、热力学和天文学等多个领域。他是数学界的巨人,在代数学以及其他数学领域都取得了卓越的成就,他的贡献影响深远,受到世人的推崇和尊敬。
总结
高斯是一个伟大的数学家,他的研究成果为代数学的发展做出了重大贡献。本文介绍了他在代数学中的成就,包括高斯整数、代数方程、线性代数、最小二乘法、复变函数、调和函数、概率论等方面。这些研究成果不仅促进了数学理论的发展,也为许多实际问题的解决提供了基础和方法。我们应该对高斯的贡献保持敬意,并且继续推动代数学的发展,为人类的未来做出更多的贡献。
如果您对本文有任何疑问或建议,欢迎在评论区留言,我们将非常乐意与您进行讨论!同时,如果您觉得本文对您有所帮助,欢迎收藏本文并关注我们的账号,我们将为您带来更多有价值的知识和信息。谢谢!
-

- 克罗地亚女总统:貌美真性情,自费看球赛,与马克龙互动很热情
-
2025-08-19 20:51:19
-

- 韩国东大门批发档口开进上海新天地
-
2025-08-19 20:49:04
-

- 采访前南斯拉夫的那座“桥”
-
2025-08-19 20:46:50
-

- 2024年度潍坊实验中学跃动轨迹精彩回顾
-
2025-08-19 20:44:36
-

- 《起风了》堀越二郎对妻子到底是薄情还是深情?
-
2025-08-19 20:42:22
-

- 历史上的各国国旗南部非洲篇(一)
-
2025-08-19 20:40:07
-

- 《伪装者》于曼丽&明台:那一场注定不可能的爱情
-
2025-08-19 20:37:53
-

- 老鼠嫁女,智慧与勇气的胜利,“共创”才有美好未来
-
2025-08-19 20:35:39
-

- 演员王耀庆:娶初恋郭晏青,22年宠妻如宝,拍戏赚的钱都给妻子管
-
2025-08-19 20:33:25
-

- 繁花如嫣——唐嫣全图写真合集
-
2025-08-19 20:31:10
-

- 岳红:那个从风雨中走出来的女人,用坚韧书写不平凡的人生!
-
2025-08-19 20:28:56
-

- 比勤奋更重要的,是深度的思考能力。
-
2025-08-19 20:26:42
-

- 35部童年动画片,你都看过几部?
-
2025-08-19 20:24:28
-

- 高铁无座票原来不是站票!买了无座票的人,不要全程傻乎乎站着了
-
2025-08-19 20:22:13
-

- 飞艇曾风靡全球,为何在80年前突然消失了
-
2025-08-19 20:19:59
-

- 酷儿理论是什么?
-
2025-08-19 20:17:45
-

- 18所广西二本大学 部分学校只需300多分 地区性大学更受欢迎
-
2025-08-19 20:15:31
-

- 厦门天竺山森林公园
-
2025-08-19 20:13:16
-

- 清朝灭亡才一百余年,上千万的满族人,为何满语迅速消亡了?
-
2025-08-19 20:11:02
-

- 李纯治国智慧大揭秘:从政治危机到经济复兴的转折
-
2025-08-19 20:08:47








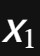
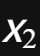
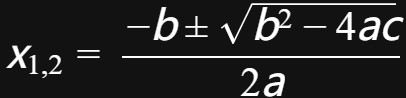
 一口气看完朱元璋二十六个儿子的生平结局
一口气看完朱元璋二十六个儿子的生平结局 史上最严重的核污染事件——切尔诺贝利事故
史上最严重的核污染事件——切尔诺贝利事故